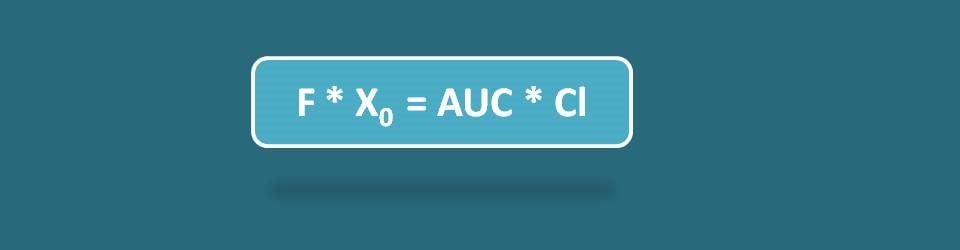Calculation of Area Under Curve (AUC)

When a drug is administered by oral route and its plasma concentrations were measured time to time, we can draw a plot of plasma concentration vs time profile of the drug which indicates the time course of the drug in the body. What is the area under this curve indicates in the plot?

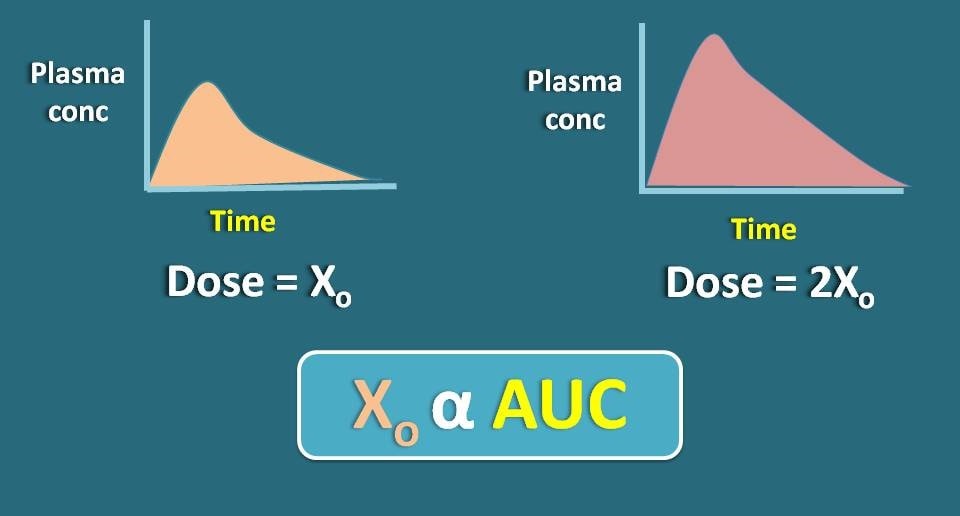
Here we can apply simple logic. Suppose we have increased dose of the drug which shows linear kinetics, the plasma concentration of the drug is also relatively increases resulting in increase in the area under curve. In another words, the dose of a drug is directly proportional to the AUC.

Note: This relation is not suitable for a drug that shows non-linear kinetics where absorption is not increased in parallel way with dose.

Formula for AUC

We know the relation between the dose X₀  and Area under curve (AUC) as

X₀ α AUC

X₀=K * AUC

Where, K is proportionality constant. But what is this K? Let’s see simplify it logically.

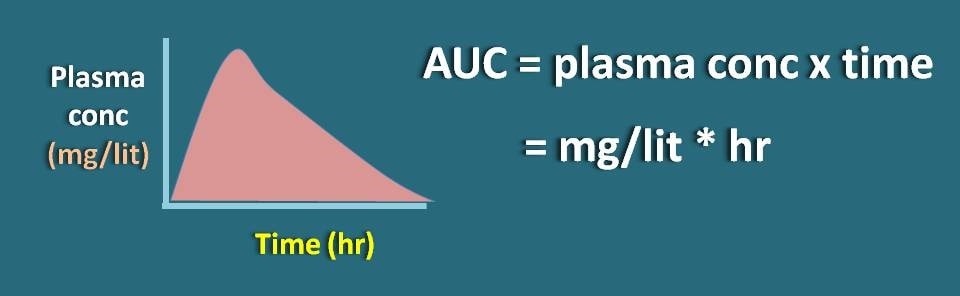
Suppose the plasma concentration of the drug is expressed as mg/lit and time in the units of hours. As the Y-axis is plasma concentration of the drug and X-axis is the time interval, area under curve will be multiple of these two parameters with units of mg/lit * hr.

If dose, X₀ is expressed in mg then what are the units of K here.

mg=K * (mg/lit) * hr

Rearranging, units of K will be lit/hr. It is nothing but clearance which is defined as the volume of the plasma from which the drug is cleared for unit time. Now the equation will,

X₀=Cl * AUC

But for many of the drugs, the entire dose may not be absorbed completely into systemic circulation. Therefore we have to introduce a term F, which indicates the fraction of the drug absorbed.

1. X₀=AUC * Cl

And as the clearance can be written as K_e * V_d the equation becomes F. X₀=AUC * K_e * V_d

Where Ke is the elimination rate constant and Vd is the volume of distribution of the drug.

Here is a vidoe on calculation of AUC.

Now let’s go with few of the working examples for calculation of AUC.

Working example 1:

The AUC of a 400 mg of drug given by oral route having 10 L/hr clearance, if 90% absorbed is

Solution:

Let’s see the data given.

Dose, X_o =400 mg

Clearance, Cl=10 L/hr

Fraction absorbed, F=90%=0.9

AUC=?

Now we can apply the following formula for calculation of AUC.

Substituting in the equation,

0.9 * 400=AUC * 10

AUC=0.9 * 400 / 10

=36 (mg/L) * hr

Let’s go with another example.

Working example 2:

A dose of 500 mg of a drug with elimination rate constant as 0.1 hr^-1 was given by oral route to achieve therapeutic concentration. If volume of distribution of the drug is 50 L and 80% of drug is absorbed, calculate AUC of the drug.

Solution:

Let’s see the data given.

Dose, X_o =500 mg

Volume of distribution, V_d =50L

Elimination rate constant, K_e =0.1 hr^-1

Fraction absorbed, F=80%=0.8

AUC=?

Here clearance is not given but we can replace it with elimination rate constant and volume of distribution. So we can use the following formula.

Substituting in the equation,

0.8 * 500=AUC * 0.1 * 50

AUC=0.8 * 500 / 5

=80 (mg/L) * hr

Now let’s how can we calculate dose of a drug required to achieve a desirable AUC.

Working example 3:

Calculate dose of a drug with half-life 0.7 hr that is required to administer to attain AUC of  25 mgL^-1 hr . The volume of distribution of the drug is 20L and 90% of drug is absorbed.

Solution:

Let’s see the data given.

t_1/2 =0.7 hr

AUC=25 mgL^-1hr

V_d=20 L

F=90%

X₀  =?

Here elimination rate constant is not given which we can calculate from the half life by using the following formula. So,

K_e=0.693 / 0.7

=0.99 hr^-1

Now let’s calculate dose required.

0.9 * X₀=25 * 0.99 * 20

X₀=25 * 0.99 * 20 / 0.9

=550 mg

So that’s about the calculation of area under curve for a drug given by oral route. Similar equations can be applied to the drugs given intravenous route where the fraction of bioavailability is equal to 1.