Electromagnetic radiation (EMR)

We are all living in various forms of energy among them one of the very important one being the Electromagnetic radiation. We are able to see by using visible light, we can send remote signals with infra red, we can even cook our food with microwaves, all these being different forms of electromagnetic radiation. Here we will see the general properties of these radiation along with their important applications.

What is EMR?

EMR is a form of energy each bundled with discrete packets of energy commonly known as photons. As the name indicates, it consists of two components, electrical and magnetic fields. How they align? Each component oscillates perpendicular to each other and even perpendicular to the direction of propagation of radiation.

Suppose EMR is propagating along X-axis, then electrical component and magnetic component oscillate in Y and Z-axis, all aligning perpendicular to one another.

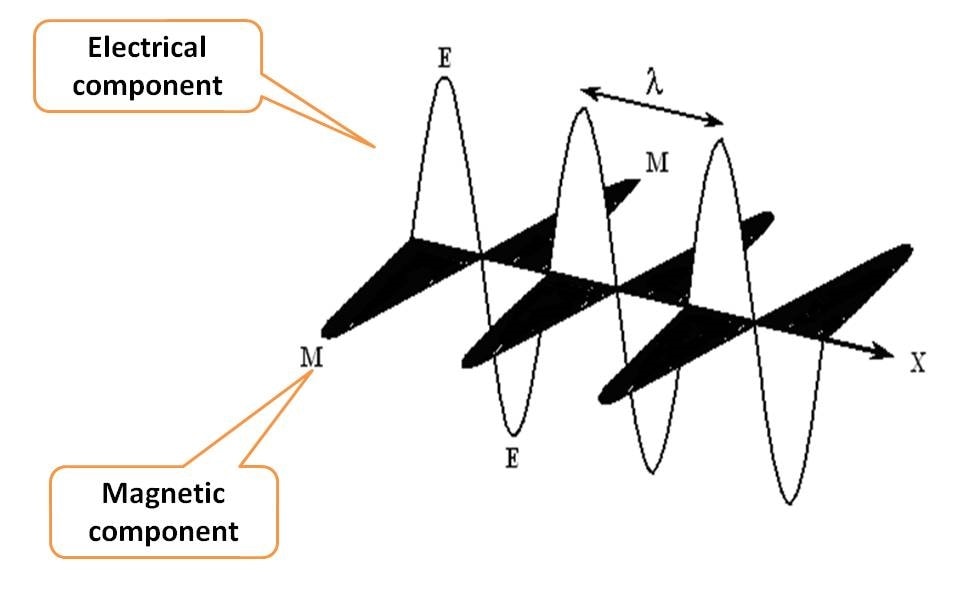
That’s great that EMR is a combination of two fields electric and magnetic, but which is important? Which is to be measured?

Undoubtedly, both are equivalent. So, if you take one into consideration you can completely characterize the particular EMR.

In order to make the process simple and easy to understand, we generally represent each EMR with a wave diagram.

Wave diagram

Wave diagram is representation of oscillations of either electric or magnetic fields that are responsible for electromagnetic radiation. Each wave diagram has highest oscillation point in upward direction called crest and in downward direction as trough.

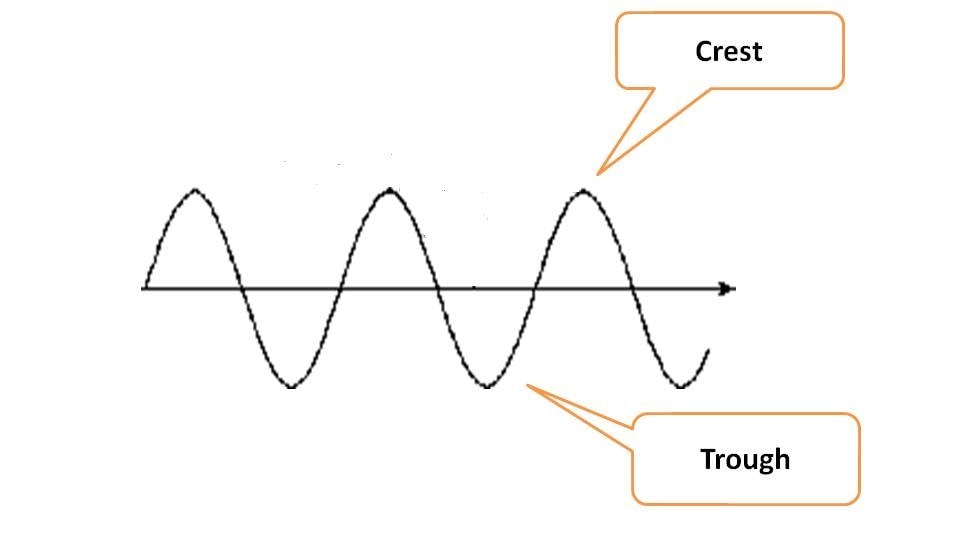
Energy always propagates in the form of wave and wave diagram has two unique characters.

Any two similar points in the wave diagram are equivalent

The maximum oscillation of upward direction is equivalent to that in downward direction.

This sounds great that if you study one wave cycle that completely denotes the entire wave. But how each wave can specifically identify a particular EMR?

Definitely that can be accomplished by defining characters of each wave. So let’s discuss here the characteristics of a wave diagram.

Characters of wave diagram

Even to define a wave and its corresponding electromagnetic radiation, one character is sufficient, here we will see all the parameters that are associated with a wave and how they can be inter convertible.

Wavelength

One of the fundamental properties that we measure for a wave is wavelength. As we know that any two similar points on the wave are equivalent, wavelength can be defined as the distance between any two equivalent points on the wave diagram.

Generally, for convenience we measure it between either two crests or two troughs. Since it is the distance, units may be meters, centimeters, micrometers, angstrom units, nanometers, picometers etc.

Here you can find how these units are inter related.

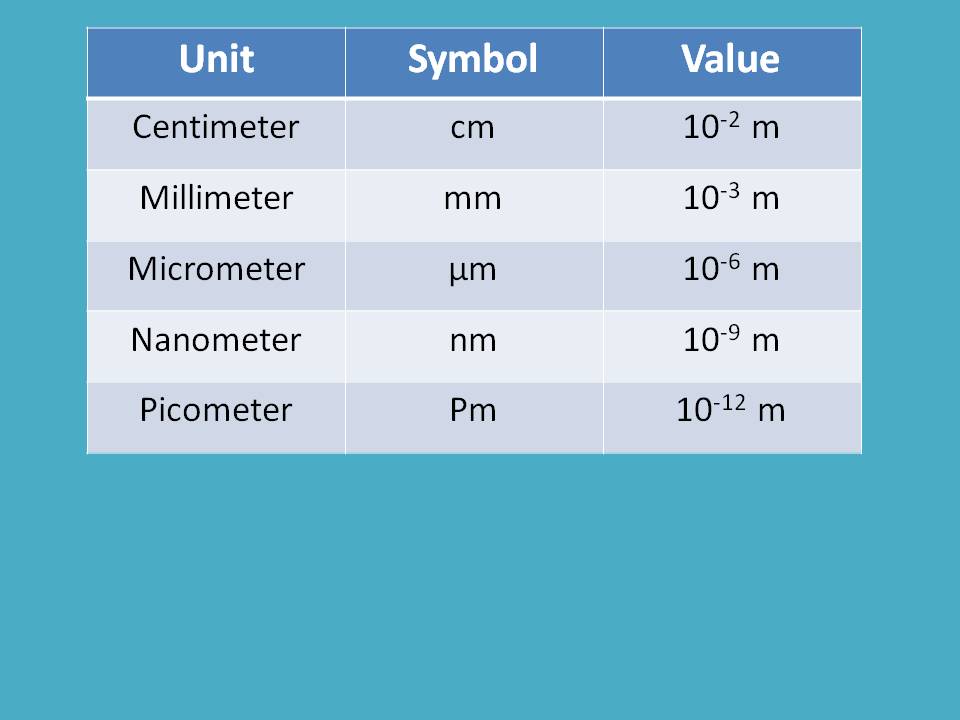
Which unit is to be selected? That all depends on the electromagnetic radiation we study. For instance, if we are dealing with UV and visible radiation, it is better to use nanometer (nm) as units. On the other hand, if we deal with IR radiation which is somewhat less energetic than UV-visible radiation, we can select micrometer (μm) as units.

Wavelength is indicated by symbol lambda (λ).

Frequency

Another parameter of wave that has wide usage is frequency. By definition, we can call it as the number of wave cycles passing though a point in one second. It is indicated by the letter ν (nu) measured in units like cycles per second (cps) or Hertz (Hz).

Suppose you can move 2 feet with each your step and you need to travel totally 10 feet, how many steps you have to make? Simply it is 10/2=5. One of your friend can move only one feet with his step, then he requires 10/1=10 steps to reach the target. So, you have more frequency that your friend.

In this way, frequency is an indicator of energy. Higher the frequency, higher will be the energy of electromagnetic radiation.

That’s nice. Is there any relation between wavelength and frequency? Certainly, they have. Consider the following wave diagrams.

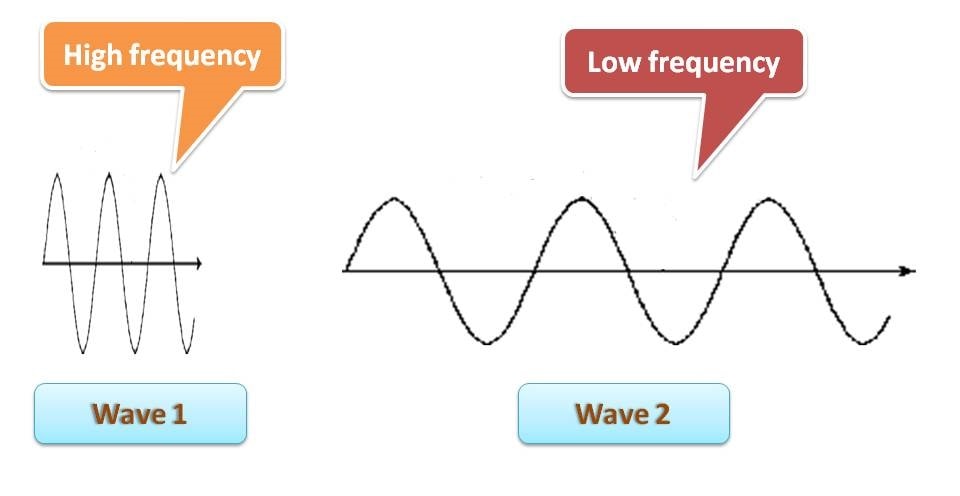
You can clearly identify that the first wave has more wavelength than the second wave. What about frequency then? It’s almost reverse. You can find that the number of wave cycles in first wave is lesser than that in second wave. In another words, frequency is more for second wave. So we can conclude that

Frequency is inversely proportional to wavelength. Higher the frequency lower will be the wavelength.

 =1/ λ

When we add proportionality constant, it becomes

 =C / λ

Where C is the velocity of the light in vacuum which is equal to 299792458 m/s = 3 x 10⁸ m/s approximately.

This velocity of the light is constant until unless the medium is vacuum. But in reality, EMR is associated with air other medium. Is there any change in the velocity of EMR then? Definitely, the velocity decreases due to some obstruction. Fortunately, the velocity of light is almost nearer to that in vacuum.

Relative velocities of light in two different medium can be measured by refractive index which is defined as the ratio of velocity of light in two medium.

For air, refractive index is 1.0003.

 

Amplitude

It is maximum oscillation of each wave on either side of the wave diagram. It is measured as the maximum height of either crest or trough. Within the spectroscopy, amplitude has no significant role.

Energy

Energy of an electromagnetic radiation is not a fundamental character to define a wave as it depends on either frequency or wavelength.

As we have discussed earlier, energy is directly proportional to frequency.

E α ν

Again adding proportionality constant,

E=hν

Where h is plank’s constant which is equal to 6.62618x10^-34 J·s

As we know that ν=C / λ ,

E=hC / λ

 

Wave number

In few situations we need another parameter, wave number, that can be obtained from other parameters. For example, infra red (IR) radiation can range from 750 nm to 0.1 mm in terms of wavelength. Here you can find that we can’t measure the wavelength in same units throughout the spectral region and we may use nm, μm and mm as units.

To make all these units in uniform way, wave number can be used. It is simply reciprocal of wavelength.

ν=1 / λ

It can be measured in units of cm^-1. Now we can define the IR range from 14000 cm^-1 to 100 cm^-1 in terms of wave number.

Note: 750 nm corresponds to 13333 cm^-1  but not equal to 14000 cm^-1

Generally, IR spectra is expressed from 14000 cm^-1 in terms of wave number.