Pharmaceutical calculations by alligation method
by egpat 11-06-2017
Alligation is one of the simple and illustrative methods in pharmacy to calculate the proportion of any two solutions to be mixed to prepare final solution of required concetration. It is highly useful for the pharmacy technicians to quickly estimate alligation ratio and then to prepare solutions of desired concentration from available stock solutions.
Is this method different from dilution? Yes,of course, but not completely different. When water is used as one of the solvent alligation simply becomes a dilution technique. In all other cases, alligation plays unique role in pharmacy calculations. So let's go in detail here.
Dilution vs alligation in pharmacy
Dilution is a simple method for preparing a lower concentration from a solution of higher concentration. Suppose you have a concetrated solution of 12M and you want to prepare 60 ml of 8M solution from the concetrated solution. Now you can simply dilute it with water by using the following formula.
M1V1=M2V2

So by using above equation, you can mix take 40 ml of concetrated solution and mix it with 20 ml of water to produce 60 ml of final solution. This is an easy task as we are simply using water as the second concetration.

On the other hand, many of the times we require an intermediate concentration from two different concentrations where alligation plays its role in pharmacy. The solutions should be mixed at a specific proportion in order to get required concentration.

This can't be calculated by simple dilution forumula as we are not using water to dilute the sample. Here alligation mathematics comes into the play to solve the problem. The proportion of two solution that should be mixed can be calculated as alligation ratio.
You can find few calculators available on the internet which simply gives you the output of alligation ratio and volumes.
How alligation works?
Now we will go with few of the working examples on this method and different steps required for its calculation.
Let’s start our discussion with a simple example.
Working example 1:
How many parts of 10% w/v solution and 4% w/v are to be mixed to produce 8%w/v solution.
Solution:
Step 1: Identify the data given.
Higher concentration=10% w/v
Lower concentration=4% w/v
Required concentration=8% w/v
What is required ? Alligation ratio=?
Step 2: Convert all the data into similar form and units
Here all the concentration terms are expressed in % w/v terms, hence no need to convert the format.
Step 3 : Apply alligation
Let’s indicate alligation ratio as H:L
Now to apply this method, subtract required concentration from higher concentration
H=8-4=4
Similarly, subtract lower concentration from required concentration
L=10-8=2

Hence alligation ratio is=H : L =4 :2=2:1
Watch here a video explaining alligation method along with examples.
Working example 2:
How many grams of 1.5 sp. gravity ointment should be mixed with 1.2 sp.gravity ointment to produce 15 gm of 1.3 sp.graviy ointment.
Solution:
Now let’s go another step in this pharmaceutical calculation i.e. to find out the weights of ointments to be mixed.
Step 1: Identify the data given.
Higher concentration (sp. gravity)=1.5
Lower concentration (sp. gravity)=1.2
Required concentration (sp. gravity)=1.3
What is required
Alligation ratio=?
Alligation volumes=?
Step 2: Convert all the data into similar form and units
Here again all the concentration terms are expressed in % w/v terms.
Step 3 : Apply alligation
Now applying the method,
H=1.3-1.2=0.1
Similarly,
L=1.5-1.3=0.2
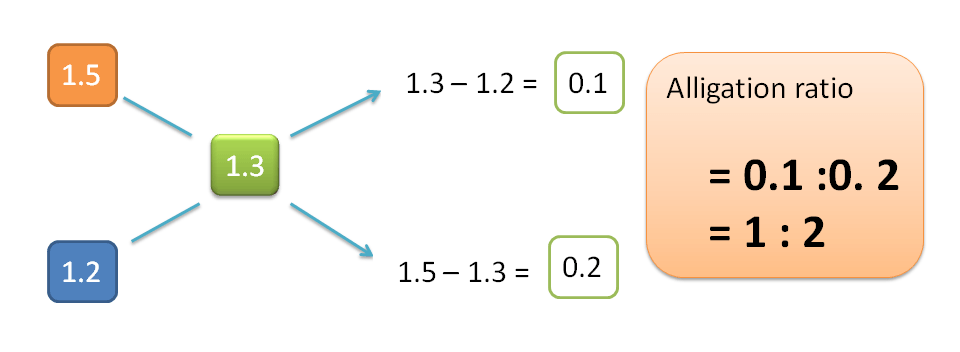
Hence alligation ratio is=H : L =0.1 : 0.2=1:2
Therefore 1 part of 1.5 sp. gravity ointment should be mixed with 2 parts of 1.2 sp.gravity ointment.
Step 4 : Calculate individual weight/volumes to be mixed
The weight of the higher concentration can be calculated by the following formula
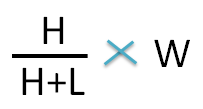
Since final weight of ointment is 15 g,the weight of the 1.5 sp gravity ointment required is
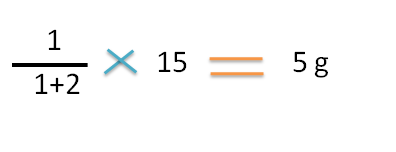
Similarly, the weight of lower concentration can be calculated by the following formula.
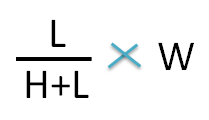
Hence the weight of 1.2 sp gravity ointment required is
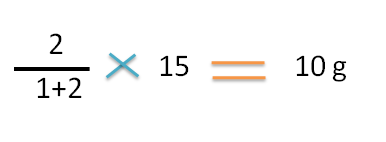
Hence 5g of 1.5 sp gravity ointment should be mixed with 10g of 1.2 sp.gravity ointment to prepare 15g of 1.3 sp.gravtiy ointment.
Working example 3:
Alligations – Solution volumes
How many millilitres of drug suspensions containing 80 mg/5 mL and 30 mg/5ml should be mixed with to prepare 500 mL of a suspension of 10mg /ml
Solution:
Step 1: Identify the data given.
Higher concentration=80 mg/5ml
Lower concentration=30 mg/5ml
Required concentration=10 mg/ml
Final volume=500 ml
What is required
Alligation ratio=? and Alligation volumes=?
Step 2: Convert the two different concentrations into similar form and units.
Here two initial concentrations are given as gm per 5ml (80 mg/5 mL and 30 mg/5ml) whereas final concentration as gm/ml (10mg /ml).
Let’s convert all in equal format.
Higher concentration is 80 mg/5 mL =16mg /ml
Lower concentration is 30 mg/5 mL =6mg /ml
Step 3 : Apply alligation
Now applying the method,
H=10-6=4
Similarly,
L=16-10=6
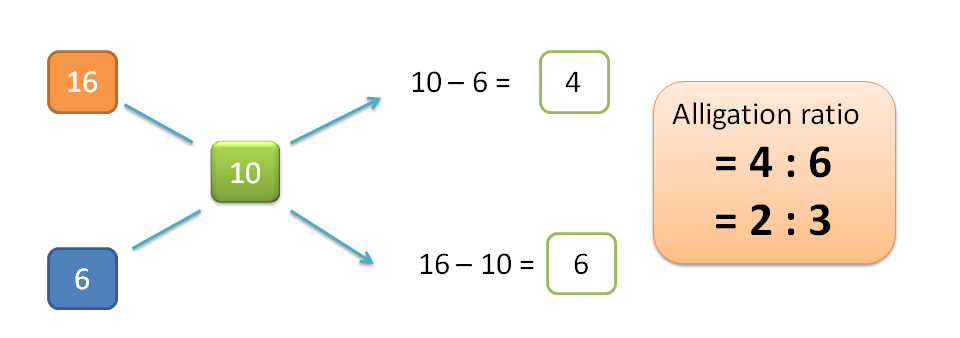
Hence alligation ratio is=H : L =4 : 6=2:3
Therefore 2 parts of 80mg/5ml suspension should be mixed with 3 parts of 30mg/5ml suspension.
Step 4 : Get the volumes required
The fraction of higher concentration in mixture is= 2 / (3+2)
The fraction of lower concentration in mixture is= 3 / (3+2)
Final volume=500 ml
Hence the part/volume of higher concentration required is
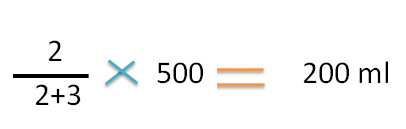
Similarly the part/volume of lower concentration required is

Working example 4:
Alligations – Solution volumes
How many millilitres of a 1:20 v/v solution of a drug is can be prepared from 100 mL of 6% v/v solution
Solution:
Step 1: Identify the data given.
Since the diluting solution is not given it can be considered as water. Hence lower concentration is treated as 0% v/v.
Higher concentration=6% v/v
Lower concentration=0% v/v
Required concentration=1:20 v/v
Higher concentration volume=100 ml
What is required
Alligation ratio=?, Alligation volumes=? and Final volume=?
Step 2: Convert the two different concentrations into similar form and units.
Here we can clearly observe that all concentration terms are not expressed equal. Higher and lower concentrations are expressed in percentage (6% v/v) whereas required concentration is expressed in the ratio (1:20 v/v).
Let’s convert required concentration in to percentage expression.
The term 1:20 indicates 1 parts of solute in 20 parts of solution.
Hence 20 ml of solution contains 1ml of drug.
100 ml of solution contains
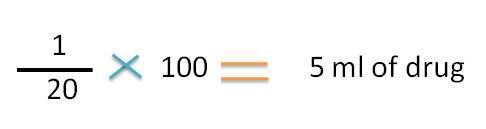
Now the concentrations are,
Higher concentration=6% v/v
Lower concentration=0% v/v
Required concentration=5% v/v
Step 3 : Apply alligation
Just as above,
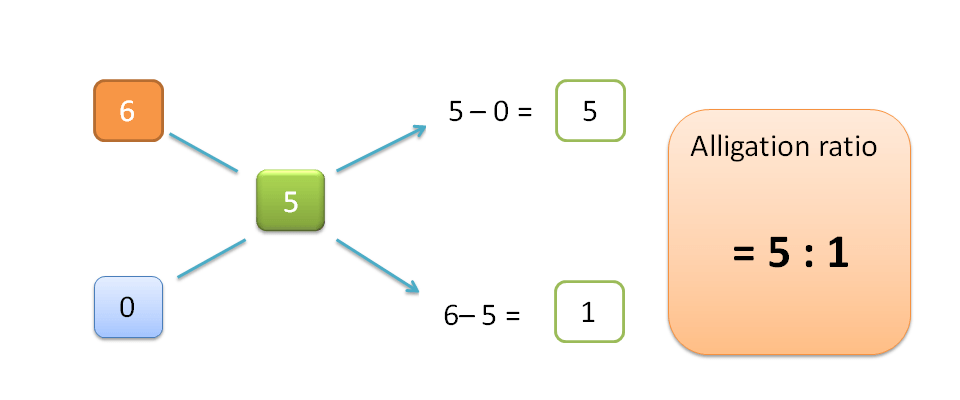
H=5-0=5
Similarly,
L=6-5=1
Hence alligation ratio is=H : L =5 : 1
Therefore 5 parts of 6% v/v solution should be mixed with 1 part of water to produce 5% v/v solution.
Step 4 : Calculate individual volumes to be mixed
The volume of the higher concentration =100 ml
By substituting in the formula,
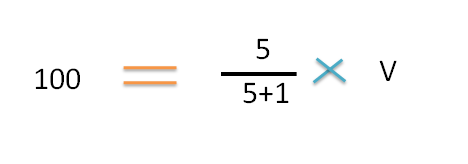
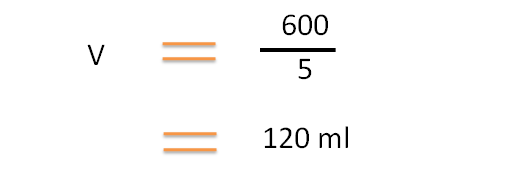
Hence a total volume of 120 ml of 5 % v/v solution can be prepared from 100 ml of 6% v/v and 20 ml of 0% v/v (water).
So, that’s about the one of the interesting method in pharmaceutical calculations. Please share this article, if you like.